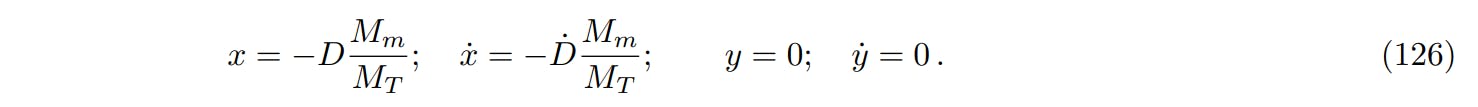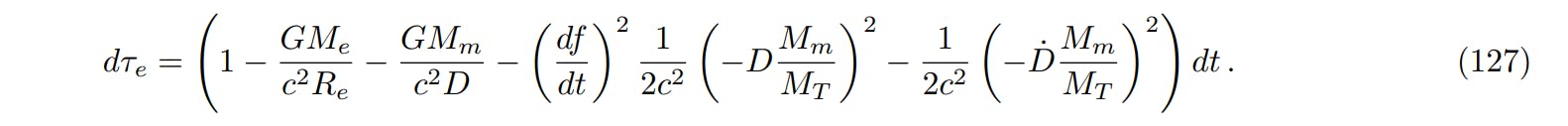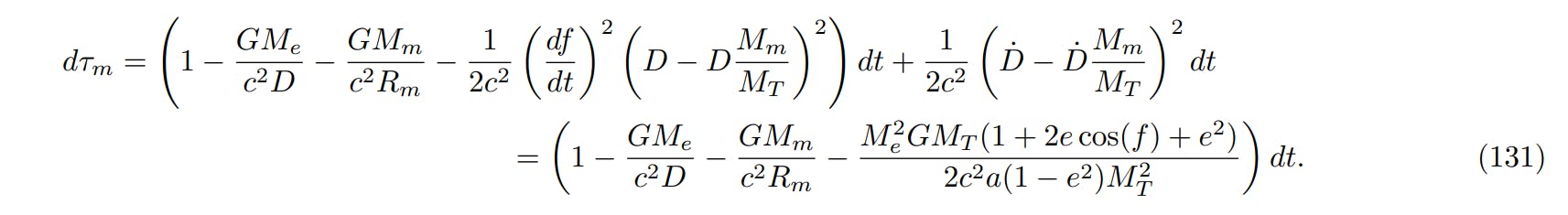Save time in space: comparison of rotating tires and self -deficiency

Links table

Abstract and 1. Introduction

2. The watch is in orbit

   2.1 Time Format

   2.2 The domestic frame for the moon

3. Differences of the average clock between the earth and the moon

4. Watch at Lagance points on Earth

   4.1 The watch in Lagrang Point L1

   4.2. The watch is in Lagrang Point L2

   4.3. The watch is in Lagrange Point L4 or L5

5. Conclusions

Approach 1: Fermi coordination with the original in the center of the moon

Approach 2: Building the center of the bloc frame freely

Things 3: Earth and moon movement equations

Approach 4: Comparing the results in rotating and non -periodic coordinates systems

Thanks, appreciation and references

Approach 4: Comparing the results in rotating and non -periodic coordinates systems

We calculate the fracture difference between the clock on the surface of the moon and the watch on the surface of the Earth in three different coordination systems. These are (1) locally self -deficiency system; (2) A rotating system in which X-Axis is along the Lunar Line Earth; And (3) translated roundabout in which the Earth is in the origin of coordinates and the moon line in the Earth in the direction x. We show that in all three coordinate systems, the fracture rate difference is the same. Keplerian is supposed to be the Earth’s system. To simplify accounts, we assume that the watches are on the roofs of the concerned bodies. This is approximation that can be improved when determining the actual areas of the watches.

4.1 Coordination Self -Deficiency System at the Bloc Center

The fixed numerical numbers in the frame of self -deficiency, which is originally in the center of the Earth’s system, neglects the terms of the tidal and the islands

The difference in the last term is a difference in squares of speeds.

4.2 The coordinates of the rotating bloc center

Provide a dowry system with a dowry line along the new X -Axis:

x x cos (f) – y sin (f);

y = x sin (f) + y cos (f);

T = t.

then

It becomes a numerical fixed

For an hour on the surface of the moon,

For an hour on the surface of the moon, there is no contribution from the term Sagnac. The right time break is

Note that there is a great contribution of the centrifugal capabilities. For an hour on earth,

The right time interval then

The right -breaking chronological time difference reduces exactly the expression in EQ. (120).

4.3 The coordinates with the Earth originally

This means using a coordinate system in which the Earth does not move. This should be a rotating coordination system with its origin coinciding with the center of the Earth. So translating the original into the center of the earth, without change in the time variable,

It becomes a numerical fixed

The capabilities were suppressed in the last chapter because it does not contribute to the arrangement of this account. For an hour on the surface of the moon,

There is no contribution from the term Sagnac but there is a great contribution from the capabilities of the centrifugal, which represents the transverse speed of the moon. The radial speed of the moon comes from the spatial part of the scale. The right time break for such an hour

For an hour on the surface of the earth,

x ′ = y ′ = x ′ = y ′ = 0.

The right time break is

It is easy to see that the appropriate fracture chronology reduces pre -derived expressions.

Thus in all three coordinate systems, the appropriate fractional time difference is the same.

Thanks and appreciation

We would like to admit the funding we received from the NNH12at81i grant. We are grateful to Elizabeth Donley, who carefully and cash carefully and made valuable suggestions. We also would like to express our gratitude to Coriel Grillge to start discussions about the moon’s time. We extend our sincere thanks to Roger Brown, Thomas Hefner, Judah Levin, Jeffrey Sherman and Daniel Slischer for their review of the manuscript. This work is the contribution of NIST and is not subject to copyright.

---

[1] Artemis Plan: Overview of the Moon Exploration Program in NASA, https://www.nasa.gov/sites/default/files/atoms/files/ Artemis PLAN-20200921.pdf, September 2020

[2] Einstein, a. Albert Einstein papers collected, Volume 6: Berlin years: Writings, 1914-1917 Princeton University Press, 1996.

[3] Park RS, Folkner WM, Williams JG, Boggs DH, Jpl Planetary, Lunar Ephemerides De440 and De441, AJ. 161 105, 2021

[4] Ashby N, relative in the GPS system, Lev. Relative priest 6, [Online Article]September 14, 2023, http://www.livingrews.org/LRR-2003-1.

[5] The International Astronomical Union (IAU), the twenty-fourth general assembly facts, “IAU Transactions, XXIVB, pp. 34-572000

[6] Ashby n and bertotti b, relative effects in local self -deficiency tires, phys. Rev. D 14 (8), 1986 (APPENDIX), 2246-2259.

[7] Ashby N and Allan D, the practical effects of the world time scale, radio science 14, 1979, pp. 649-669.

[8] BERTONE, S, Arnold, D, Giradin, V, Lasser, M, Meyer, U, J¨aggi, A, Evaluation of low dynamic standards to determine the orbit of the cup and restore the solutions of the independent lunar gravity, Earth and space science, 2021, https: // Doi.org/10.1029/20201454.

[9] Ries JC, Eanes RJ, SHUM CK, Watkins Mm (20 March 1992). “Progressing the Earth’s gravity factor.” Geophysical research messages. 19 (6): 529-531.

[10] CoData 2006, Physics.nist.gov/cuu/CONSTANTS

[11] Mohr PJ, Taylor BN, and Newll DB, CODATA recommended values ​​for basic physical constants: 2006, Reverend Mod. Phys. , 80, pp. 633-730, 2008

[12] Konopliv AS, et al. Accuracy. Planets, 118, 1415-1434, 2013, doi: 10.1002/jgre.20097

[13] Daher, H Et al. The Earth’s long -term development with high -level tidal and ocean models, geophysical research journal: Planets, 126 (12), 2021, E2021je006875. https://doi.org/10.1029/2021je006875

[14] Petit G and Wolf P, a relative theory of time comparisons: Metrologia review, 42 (3), 2005, S138

---